“Build a man a fire, and he’ll be warm for a day. Set a man on fire, and he’ll be warm for the rest of his life.” — Terry Pratchett
The most common fire in a process plant is a pool fire. A pool of flammable liquid, something that exists normally or, more likely, something that is released unintentionally, ignites and the flames quickly spread to engulf the entire surface of the pool.
The intensity of the fire is a function of the properties of the liquid that is on fire and the area of the pool. It doesn’t matter how deep the pool is because only the surface is burning. Understanding the relationship between various properties and the surface area of the pool fire with the intensity of pool fires, then, is the key to understanding the intensity of pool fires.
The EPA’s Guidance for Offsite Consequence Analysis
When it comes to analyzing the consequences of a variety of events, one of the best places to start is the EPA’s Risk Management Program Guidance for Offsite Consequence Analysis (OCA). When the substance you are looking at is regulated under the Risk Management Planning (RMP) rule in 40 CFR 68, it makes sense because the OCA exactly complies with the requirements of the standard. There are certainly other tools available, but the OCA is readily available to anyone. More importantly, the appendices that explain how the values are derived are clear and well annotated, especially Appendix D, Technical Background. Taken together, the guidance and its appendices are an incredibly useful 256 pages.
When it comes to pool fires, the OCA has lots of tables, which allows the user to completely avoid doing any math, or for that matter, even understanding what the EPA is asking. However, there is information in Section D.9 on pool fires that explains what the EPA was thinking when it developed this guidance. One equation is especially revealing:
x = Hc [ (0.001 A 0.4 τa)/(5,000 (4π)(Hv +Cp(Tb – Ta)) ]0.5
If you’re looking at this and thinking sure, obviously, x = Hc blah, blah, blah, I don’t blame you. But there are four assumptions rolled up in that equation that are worth knowing about, particularly if you want to apply the EPA method to flammable liquids that are not regulated by the RMP rule. Why would you do that? Not because regulations required you to, but because you want to understand the hazards in your facility, say for a facility siting study.
So, what are these four assumptions?
- The term “A”, which refers to the area of the pool fire, in m2.
- The term “0.4”, which refers to the fraction of combustion energy dissipated as thermal radiation.
- The term “τa”, which refers to the atmospheric transmissivity of thermal radiation.
- The term “5,000”, which refer to the radiation level, in Watts/m2.
Knowing where those terms come from and how they might be adjusted will allow you to adapt this methodology to the scenarios you are really concerned about.
Area
If the pool is contained, then the EPA allows you to use the area of the containment as the area of the pool. A perfect correlation with the real world. If the pool is not contained, then the EPA requires that you assume that it spreads out to a depth of one centimeter. The OCA mentions this one centimeter requirement 18 separate times, but never offers an explanation. Its just what the regulations says.
When considering a pool fire for a regulated flammable liquid, you must use one centimeter. When adapting the methodologies to other flammable liquids, feel free to consider the roughness and topography of your surfaces. In the absence of any other information, use one centimeter. Keep in mind, though, that it doesn’t take many pot holes to change the average depth to more, as you’ve probably noticed after a heavy rain.
Fraction of Combustion Energy Dissipated as Thermal Radiation
The OCA states that “the fraction of combustion energy dissipated as thermal radiation is reported to range from 0.1 to 0.4. To develop factors for estimating distances for pool fires, this fraction was assumed to be 0.4 for all regulated substances.” When considering a pool fire for a regulated flammable liquid, you must use a fraction of 0.4, which is clearly a conservative assumption.
When adapting the methodologies, it is important to note that the value of 0.4 is an upper limit of the data, and that the research shows that the range is not random, but strongly dependent on the size of the fire.
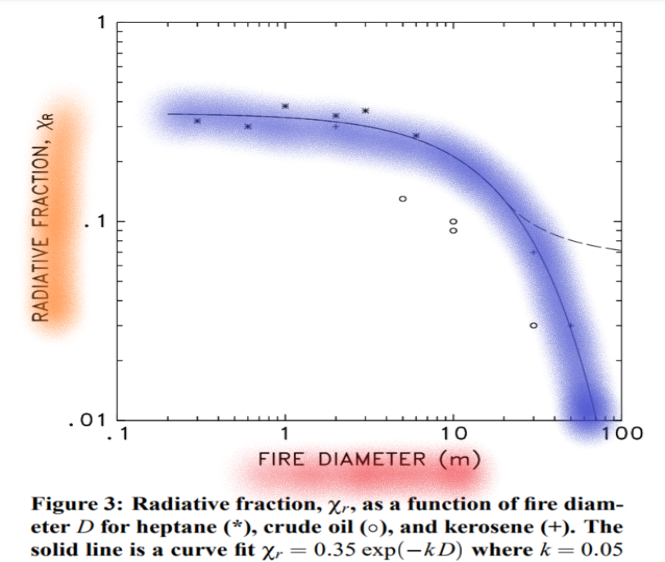
Research at the National Institute of Standards and Technology shows that the radiative fraction approaches 0.35 when a fire is very small (less than 20 cm in diameter) but drops off quite predictably as the fire get bigger. Since the area of the pool fire is defined in the EPA method, it is entirely appropriate to use the NIST equation to calculate the radiative fraction. An enormous fire (70 m in diameter) would have a radiative fraction of 0.01.
Atmospheric Transmissivity
The EPA method requires the assumption that the atmospheric transmissivity, τa, of the radiant energy be assumed to be 100%. The transmissivity of radiation through the atmosphere is dependent on the wavelength of the radiation. The atmospheric transmissivity of radio waves is 100% (the opacity is 0%), and the atmospheric transmissivity of visible light approaches 100%. But the atmospheric transmissivity of infrared, the wavelength that carries most radiant heat, is near zero.
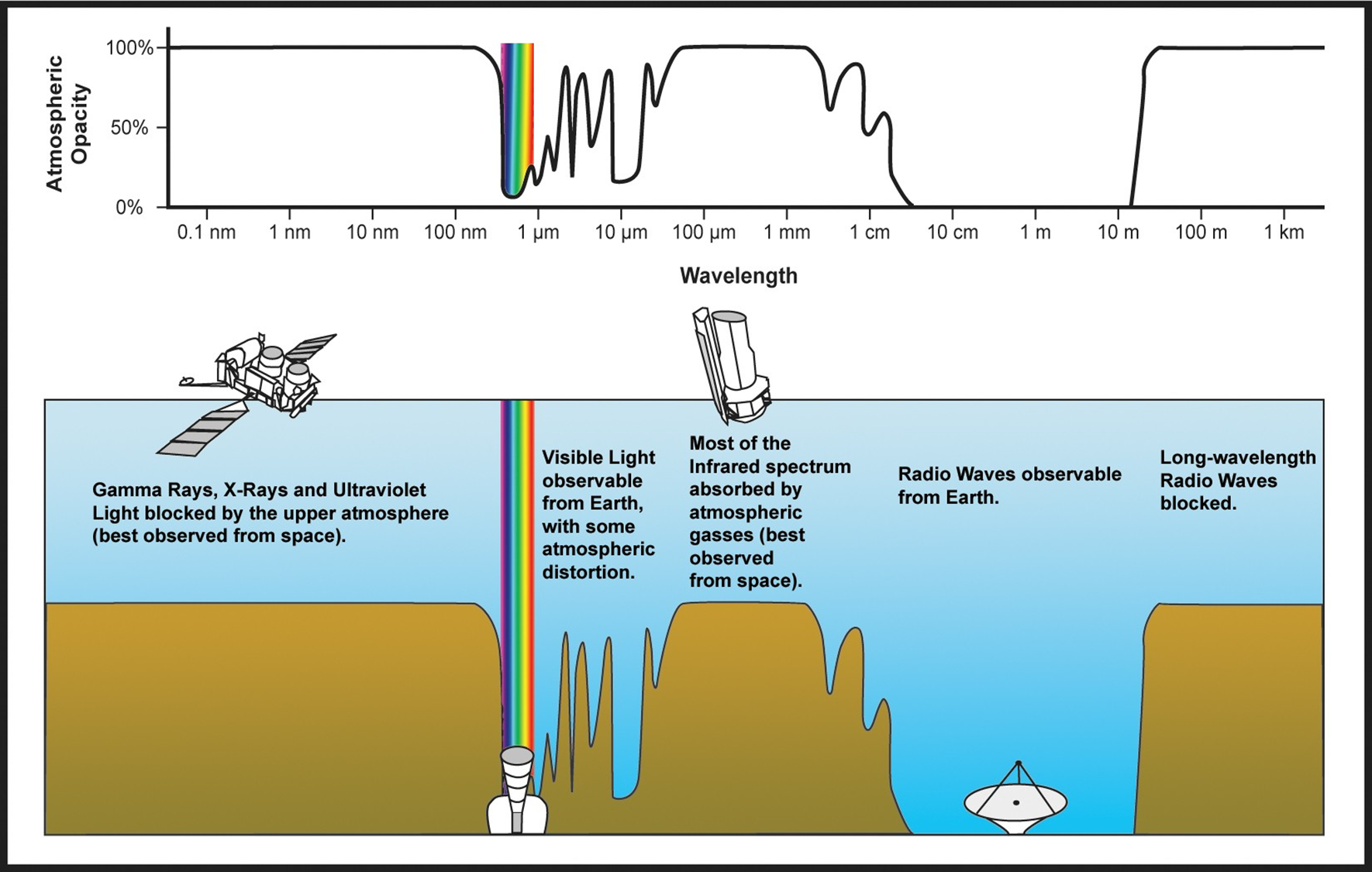
Image credit: NASA
All this assumes a clear atmosphere. The presence of smoke or water vapor increases the opacity of the atmosphere. So, the assumption of 100% atmospheric transmissivity is extremely conservative.
When adapting the methodologies, it would be reasonable to assume an atmospheric transmissivity much less than 100%. Even a τa of 0.5 would still be conservative.
Radiation Level
Finally, there is the radiation level, q. The EPA uses a radiation level of 5,000 W/m2 (5 kW/m2) as its endpoint target. This level is widely reported as the radiation level that will cause second degree burns after an exposure of 40 seconds. It’s a perfectly reasonable target.
However, there are other targets that may be of interest:
q = 1.4 kW/m2, to protect people (equivalent to sunlight) [HUD, in 24 CFR 51.203]
q = 2 kW/m2, pain within 60 sec [ALOHA]
q = 5 kW/m2, second degree burns within 60 sec [ALOHA]
q = 10 kW/m2, lethal within 60 sec [ALOHA]
q = 12.5 kW/m2, wood produces ignitable volatiles [Lee’s Loss Prevention]
q = 25 kW/m2, wood ignites [Lee’s Loss Prevention]
q = 31.5 kW/m2, to protect structures [HUD, in 24 CFR 51.203]
q = 37.5 kW/m2, damages process equipment [Lee’s Loss Prevention]
When adapting the methodologies, choose a radiation level that is consistent with the scenario of concern. It may not be 5,000 W/m2.
When Conservative Assumptions are Pile Up
An accepted approach to risk assessments is to be conservative. This is completely understandable; we should be conservative, especially when we are uncertain. That conservatism, however, should apply to our target, not to our analysis. During our analysis, we should be as accurate as we are able. One of the pitfalls of risk assessments is the accumulation of conservatism.
In cost assessments, there is frequently a tendency to add a 10% margin for uncertainty. As every person contributing to the assessment add their uncertainty margin, it quickly compounds. It is not uncommon for the final estimate to be twice what it should have been because of this compounding of uncertainty margins.
In risk assessments, however, the tendency is not to add 10%, but to double or triple the values “for safety”. When these are compounded, the final risk assessment can be increased by one or two orders of magnitude.
Go Ahead, Use the OCA for Your Own Purposes
The approach to pool fires that the EPA developed is straightforward and simple to use. It doesn’t require extensive modelling or computing power, and it is easy to understand. Use it. When you are using it to understand pool fires outside the scope of an RMP plan, however, don’t feel like you must accept all the conservative assumptions that the EPA made in order to make their tool universal. Adapt the method to your own needs.
